- Search
| Neurospine > Volume 18(3); 2021 > Article |
|
|
Abstract
Objective
The lordotic shape of the lumbar spine differs substantially between individuals. Measuring and recording strain during spinal biomechanical tests is an effective method to infer stresses on spinal implants and predict failure mechanisms. The geometry of the spine may have a significant effect on the resultant force distribution, thereby directly affecting rod strain.
Methods
Seven fresh-frozen cadaveric specimens (T12-sacrum) underwent standard (7.5 Nm) nondestructive sagittal plane tests: flexion and extension. The conditions tested were intact and pedicle screws and rods (PSR) at L1-sacrum. The posterior right rod was instrumented with strain gauges between L3–4 (index level) and the L5–S1 pedicle screw. All specimens underwent lateral radiographs before testing. Lordotic angles encompassing different levels (L5–S1, L4–S1, L3–S1, L2–S1, and L1–S1) were measured and compared with rod strain. Data were analyzed using Pearson correlation analyses.
Results
Strong positive correlations were observed between lordosis and posterior rod strain across different conditions. The L3–S1 lordotic angle in the unloaded intact condition correlated with peak rod strain at L3–4 with PSR during flexion (R=0.76, p=0.04). The same angle in the unloaded PSR condition correlated with peak strain in the PSR condition during extension (R=-0.79, p=0.04). The unloaded intact L2–S1 lordotic angle was significantly correlated with rod strain at L3–4 in the PSR condition during flexion (R=0.85, p=0.02) and extension (R=-0.85, p=0.02) and with rod strain at L5–S1 in the PSR condition during flexion (R=0.84, p=0.04).
The lordotic shape of the lumbar spine differs substantially between subjects and is intimately related to spinopelvic geometry [1]. Lumbar curvature disturbance is potentially involved in the genesis of several spinal disorders, rendering the study of sagittal balance critical for planning spine surgery. Restoration of lumbar lordosis (LL) is an essential element of spinal deformity correction surgery and has a direct impact on clinical outcomes [2-6].
The upper arch of LL is more constant, whereas the lower arc is more variable and plays a greater role in overall lordosis. The lower arc also corresponds with and reacts to the sacral slope angle. Mild changes in any of these factors can dramatically affect the distribution of mechanical loading in the entire spine, pelvis, and lower limbs [7-11].
The failure to restore the ideal LL shape might be associated with postoperative mechanical failures on long-segment constructs, such as pseudoarthrosis or rod fracture [12]. Excessive postoperative lordosis has also been reported to be a potential cause of mechanical failure [13,14]. In spite of extensive efforts investigating the clinical relevance of sagittal balance, the rate of rod fractures remains high [14-16].
Measuring strain during spinal biomechanical tests effectively infers the stresses on spinal implants and predicts failure mechanisms [17]. Strain is the ratio of change of the material length to the initial length in response to the application of force [18,19], with low strain rates on implants associated with better outcomes and lower rates of mechanical failures [20]. In solid mechanics, the resulting stress and strain distributions through a load-bearing structure depend not only on the applied load but also on the shape of the structure. However, no previous biomechanical study has analyzed the effect of LL or the shape of a surgical construct on the resultant instrumentation strain during loading. In the current study, we hypothesized that the geometry of the lumbosacral spine may have an impact on the resultant force distributions during loading, directly affecting rod strain (measurable using strain gauges).
Seven fresh-frozen lumbar spine cadaveric specimens (T12-sacrum) were studied (n = 7). The same specimens were also part of a separate study conducted in our laboratory to assess the subsequent stability and rod strain of different construct designs during anterior column realignment [21]. Informed consent was not needed because this was a cadaver study, and Institutional Review Board approval was not sought due to the nature of the investigation. Donor medical records and plain film radiographs were reviewed, and direct manual inspection was performed to ensure that the specimens had no obvious pathologic conditions. Dual-energy x-ray absorptiometry scans were performed to assess bone mineral density (Table 1) [21].
Specimens were stored at -20°C until test day and then thawed in normal saline at 21°C. Muscles and soft tissues were cleaned while keeping intact all ligaments, joint capsules, and intervertebral discs. The sacrum was reinforced with household wood screws placed in a rectangular metal mold and embedded using fast-curing resin (Smooth-Cast; Smooth-On, Easton, PA, USA) to permit attachment to the base of the testing apparatus. The top vertebra (T12) was also reinforced with household screws and embedded in the same resin in a cylindrical-shaped pot (≈200 g) for test frame attachment and loading.
In all cases, polyaxial pedicle screws with a cobalt-chrome head and titanium alloy shaft (Ti-6A1-4V) were used (L2–5: 6.5 × 45–55 mm, S1: 7.5 × 55 mm; NuVasive, San Diego, CA, USA). Cobalt-chrome rods were chosen over titanium because they have been gaining importance in the adult spinal deformity surgery setting. Two 5.5-mm diameter cobalt-chrome rods were contoured bilaterally to fit screw heads from L1 to S1 to minimize the need for reduction. We did not intend to change the lordosis curvature when the rod was locked in place, although minimal changes can always occur during the implantation.
In each case, a robotic 6-degree-of-freedom apparatus test frame was used to apply standard nondestructive pure moment loads up to 7.5 Nm at a mean global rotation rate of 1.5° per second [22]. The pure moments were applied in the sagittal plane: flexion and extension. Using pure moments has the advantage of distributing the same load to each level of the spine, ensuring an equivalent comparison among all levels, regardless of the distance from the point of loading [23,24].
During all tests, 3-dimensional motion measurements were made with the Optotrak 3020 camera apparatus (Northern Digital, Waterloo, Ontario, Canada). This system stereophotogrammetrically measures 3-dimensional displacement of infrared-emitting markers rigidly attached in a noncollinear arrangement to each vertebra at the ends of three 4-cm surgical guide wires drilled into each vertebral body. Range of motion was measured using custom software to convert the marker coordinates to angles about each of the anatomical axes [25]. The conditions tested were (1) intact and (2) pedicle screws and rods (PSR) at L1-sacrum.
Because there were no statistically significant differences between right-side and left-side rod strains in a previous study [26], only right-side rod strain was monitored in the current study. Rods were instrumented with stacked rosette strain gauges (CEA06-062UW-350/P2, Vishay Micro-Measurements, Raleigh, NC, USA) at the index level (L3–4) and at the lumbosacral junction (L5–S1), with the gauges facing posteriorly. The gauges were positioned at the midpoint distance between L3 and L4, as well as at the L5 and S1 pedicle screw heads, respectively (Fig. 1). Strain on the posterior rods during specimen loading was recorded at 10 Hz using the StrainSmart data acquisition system (Vishay Micro-Measurements, Raleigh, NC, USA). Only the vertical or longitudinal component strains were used for analysis.
The specimens underwent lateral radiographs, and LL encompassing different levels (L1–S1, L2–S1, L3–S1, L4–S1, and L5–S1) was measured using the Cobb method in all different spine conditions before loading (Fig. 2). Angles were measured using the sacral endplate and the superior endplate of each lumbar vertebra with exception of L1, which was measured using the inferior endplate. The films used were not large enough to encompass the superior endplate of L1. The angle measurements were performed using ImageJ software (US National Institutes of Health, Bethesda, MD, USA) and encompassed the inferior endplate of the upper vertebra and the sacral endplate. The superior endplate was not used because of the inability to include the superior L1 endplate on the film for all specimens. These angles were compared with peak recorded rod strains for each test condition. Angle value comparisons between conditions were performed using paired t-tests. Data were analyzed using a Pearson product moment correlation analysis (SigmaPlot v14); p-values < 0.05 were considered statistically significant.
There were no significant differences in mean angles of the intact condition compared with the PSR condition (p>0.51), with the exception of the L4–S1 angle (p=0.01). Angles measured in intact and PSR conditions are shown in Table 2, and strain values are shown in Table 3. The mean and standard deviation (SD) rod strain value reported for L3–4 during flexion was 238.6±64.4 µε, and during extension, it was -263.9±88.1 µε. The mean and SD strain value reported for L5–S during flexion was 145.1±118.1 µε, and during extension, it was -222.7±185.9 µε. The strain values reported are within the same range as other biomechanical studies [27].
Several correlations between lordosis angles at rest and peak posterior rod strains during loading were statistically significant (Fig. 3) (p≤0.04). L2–S1 and L3–S1 lordotic angles in intact and PSR conditions were significantly correlated with rod strain at various spinal levels, conditions, and directions of loading, as shown in Table 4 and discussed below.
The L3–S1 angle measured in the intact condition at rest was significantly correlated with rod strain at L3–4 in the PSR condition during bending in flexion (R=0.76, p=0.04) and without significance during extension (R=-0.73, p=0.06). L2–S1 angles measured intact during rest correlated with rod strain at L3–4 in the PSR condition during bending in flexion (R=0.85, p=0.02) and extension (R=-0.85, p=0.02), as well as with rod strain at L5–S1 in PSR during bending in flexion (R=0.84, p=0.04). For other comparisons, correlations were not statistically significant (p≥0.05).
The correlation between the L3–S1 angle measured in the PSR condition at rest and rod strain at L3–4 in the PSR condition during bending was significant during extension (R=-0.79, p=0.04), but not during flexion (R=0.74, p=0.06). For other comparisons, correlations were not statistically significant (p≥0.05).
Human bipedalism is possible because peculiarities of the spinopelvic anatomy allow humans to reach maximum equilibrium in the erect position with minimal activation of the back muscles. The most notable of these singularities is the verticalization of the pelvis and successive opposing sagittal curvatures. LL is found in no other species; great apes can achieve an upright position but only with a semierect trunk. The extensor muscles are also critical for maintaining stability during movement. Recent modeling suggests that a spine with large lordosis requires a greater follower load in the standing position than one with minimal lordosis. Increased LL requires larger extensor musculature to provide sufficient follower loads and sagittal stability [28].
Global lordosis increases as the sacral slope becomes more vertical, demonstrating a reciprocal association between the orientation of the sacrum and the degree of LL curvature. Patients with greater pelvic incidence and sacral slope, and consequently higher LL, are predisposed to develop lumbar spondylolisthesis because of higher shear stress on posterior elements directly affecting the isthmus, which leads to failure of this structure [29]. Lumbar spines with greater curvature tend to experience increased shear forces on posterior joints. Our study results suggest a strong relationship between native lordosis and an immediate postoperative increase in rod strain, which could potentially translate into increased rod fracture rates. During rod implantation, no specific maneuver was performed with the objective to increase lordosis, and caution was taken to not change the native curvature. The rod was carefully bent to meticulously meet the screw heads without the need to reduce the spine, even though the L4–S angle following PSR was significantly smaller than the corresponding intact angle (Table 2) (p=0.01). It should be noted that this level corresponds exactly to the lower arc of lordosis, which is the most important region with regard to lumbar spine curvature.
Strain monitoring during biomechanical tests has been spotlighted recently because these measurements are a good predictor of metal fatigue and risk of rod breakage [17]. Few biomechanical studies have addressed the influence of LL on load distribution [30,31]. No previous in vitro study has addressed the influence of LL on rod strain measurements. Previous studies have, however, demonstrated that posterior rod strain can be attenuated by certain techniques [26,27]. For example, the addition of anterior column support using a cage with a large footprint at the base of the construct, or additional supplemental posterior rods, can mitigate rod strain [32]. Further studies are necessary to investigate whether these supplemental methods are influenced by variations in LL.
The correlations observed in the current study are difficult to rationalize, especially under pure moment loading. As illustrated in Fig. 4, an applied pure torsional load (i.e., bending moment) is the mechanical equivalent to a pair of applied force vectors equal in magnitude and opposite in direction. Thus the anterior spine, for example, can be considered to be in tension, while the posterior region is effectively compressed in extension (and vice versa in flexion). An online finite element analysis calculator designed and validated for 2-dimensional structural truss calculations [33], with a simplified analysis that assumes that a single posterior rod spanning 6 levels (screw locations) supports the resulting tensile or compressive load, illustrates (Fig. 5) that a rod with increased curvature (lordosis) experiences greater stress than a less-curved rod of the same length, with maximum stresses occurring at the apex region (approximately the L3–4 region). Although greatly simplified, this illustration provides a rationale for the observed increase in L3–4 rod strains with increasing lordosis.
We found significant correlations between LL and rod strain for PSR instrumentation spanning L1 to S1. This finding supports the hypothesis that, with hyperlordotic spines, the stress distributions tend to concentrate more on the posterior column in the lumbar spine. L2–S1 intact lordosis at rest correlated with increasing strain at both the index level and lumbosacral junction in the PSR condition during loading. This finding suggests that overall intact lordosis at rest can translate to instrumented strain during loading. Both intact and PSR L3–S1 lordosis at rest correlated to L3–4 rod strain in at least one direction of bending, e.g., flexion (intact lordosis) and extension (PSR lordosis).
The current study results also corroborate the general hypothesis that sagittal alignment restoration must necessarily seek an ideal spinal equilibrium, which raises a concern of possible effects from overcorrection. In a clinical study of 96 patients (74% of whom had overcorrection), Pizones et al. [13] demonstrated that 77.4% of the patients who had overcorrection developed mechanical complications compared to 15% of those who were matched to their ideal shape, or to 58% of those who ended up with undercorrection. Pizones et al. [13] also suggested that sagittal alignment should be restored to match the ideal Roussouly classification sagittal shape dictated by pelvic index [8] to decrease the rate of mechanical complications. Zhang et al. [14] performed a clinical study with 160 patients who underwent lumbar spine decompression and fusion and reported that patients who returned to the standard Roussouly type not only improved the sagittal curvature but also improved the functional score.
Although restoration of LL in adult spinal deformity has been spotlighted as an important factor for favorable surgical outcomes, excessive postoperative lordosis, or sagittal overcorrection is not desired because of the increased risk of mechanical complication [13,14]. Sebaaly et al. [34] reported that the most important factor in limiting mechanical complications is the restoration of the sagittal shape of the spine to its original profile according to the Roussouly classification. Correction techniques to the whole spine according to a simple formula involving a fixed angle and the LL might not be the ideal restoration. Lordotic apex, as well as lordosis length, which is variable and may be shorter or longer than anatomical LL, should also be considered.
This study has several limitations. The strain gauges were only able to measure rod strain at specific locations and not throughout the instrumentation. Furthermore, cadaveric biomechanical studies have well-known limitations, including the lack of muscle activities and the use of healthy spines without a target disease that might represent the indication for the studied surgical technique. The testing paradigm used herein evaluated immediate stability and strain distributions that can affect longer-term mechanical failure in the clinical scenario. Cyclic loading was beyond the scope of the current study and is problematic because it is not possible to truly simulate the long-term in vivo environment. That is, low-loading high-cycle paradigms with cadaver tissue tend to degrade the tissue before any instrumentation failure occurs. Further research is required to determine the effect of the curvature on the strain distribution throughout the lumbar spine and its repercussion on patient outcomes. A more detailed in vitro strain distribution study involving multiple levels and more complex types and direction of loads, including axial rotation, lateral bending, and compression, is recommended. Because the native L4–S1 curvature changes with a significant difference before and after the procedure, the influence of the procedure cannot be excluded.
Native LL measurements before loading demonstrated strong correlations with in vitro immediate postoperative posterior rod strains during loading. LL has a strong positive linear correlation with in vitro posterior rod strain. These relationships should be strongly considered when interpreting biomechanical test results in long-segment fusion models. Further studies are necessary to characterize and illuminate the underlying mechanisms that determine rod strain, as well as to correlate the impact of lumbar curvature correction on rod strain in clinical practice and postoperative surgical outcomes.
CONFLICT OF INTEREST
Jay D. Turner has served as a consultant for NuVasive (San Diego, CA) and SeaSpine (Carlsbad, CA). Juan S. Uribe has served as a consultant for NuVasive (San Diego, CA), SI Bone (Santa Clara, CA), and Misonix (Farmingdale, NY). Other authors have nothing to disclose.
ACKNOWLEDGEMENTS
Portions of this manuscript were presented at the North American Spine Society 34th Annual Meeting, September 2019, Chicago, Illinois; Spine Summit 2019, March 2019, Miami Beach, Florida; and the International Society for the Advancement of Spine Surgery 19th Annual Conference (ISASS19), April 2019, Anaheim, California. NuVasive (San Diego, CA) provided partial research support paid directly to the authors’ institution; Barrow Neurological Foundation (Phoenix, AZ) provided partial research support paid directly to the authors’ institution. The authors thank the staff of Neuroscience Publications at Barrow Neurological Institute for assistance with manuscript preparation.
Fig. 1.
Strain gauges used for strain measurement at the index level (L3–4) and lumbosacral junction (L5–S1). Adapted with permission from Barrow Neurological Institute, Phoenix, AZ, USA.
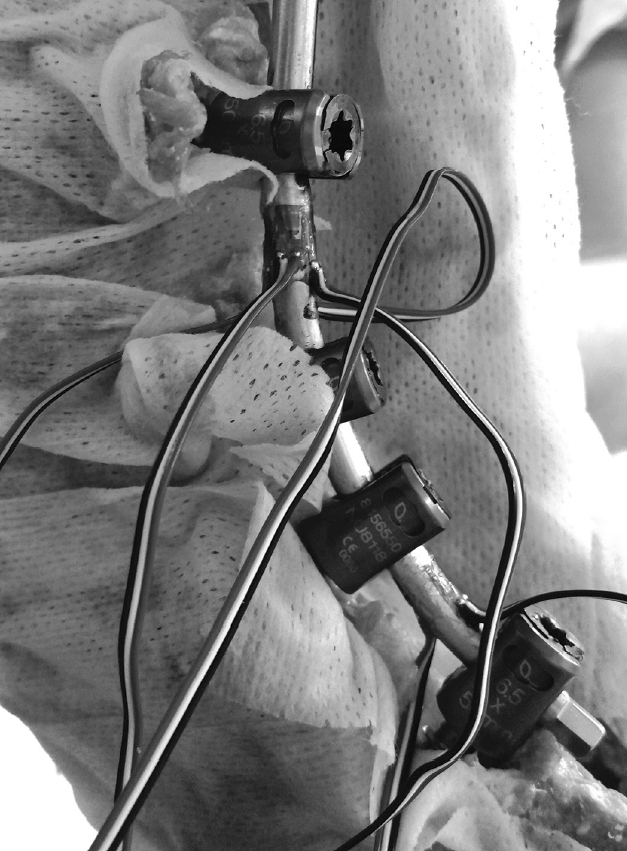
Fig. 2.
Examples of different lordosis angles measured. Adapted with permission from Barrow Neurological Institute, Phoenix, AZ, USA.
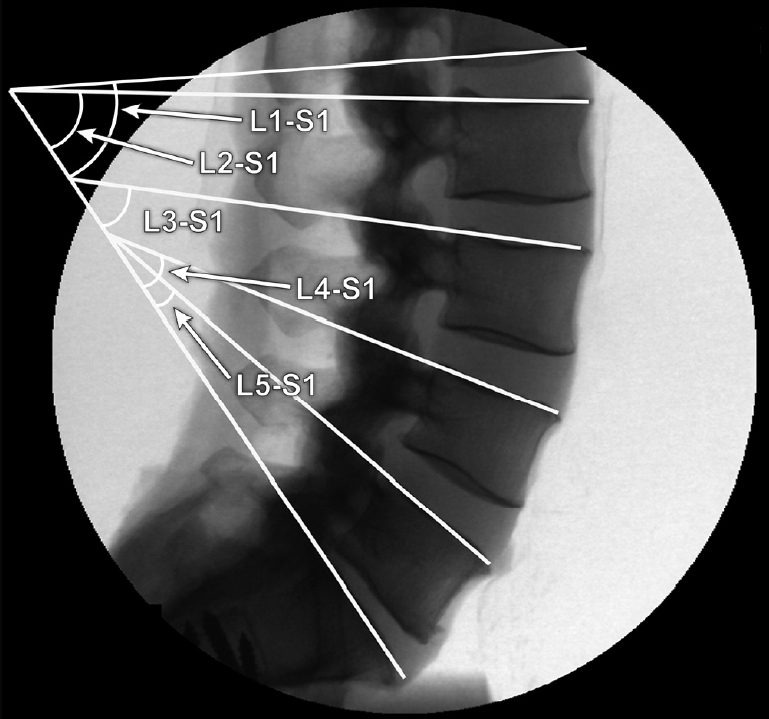
Fig. 3.
Correlations between posterior rod strain (RS) and lordotic angles in different conditions. (A) RS at L3–4 during pure moment bending versus intact L3–S1 lordosis. (B) RS at L3–4 and L5–S1 versus intact L2–S1 lordosis. (C) RS at L3–4 versus pedicle screws and rods (PSR) L3–S1 lordosis. A p-value of < 0.05 were considered statistically significant. R, coefficient of correlation. Adapted with permission from Barrow Neurological Institute, Phoenix, AZ, USA.
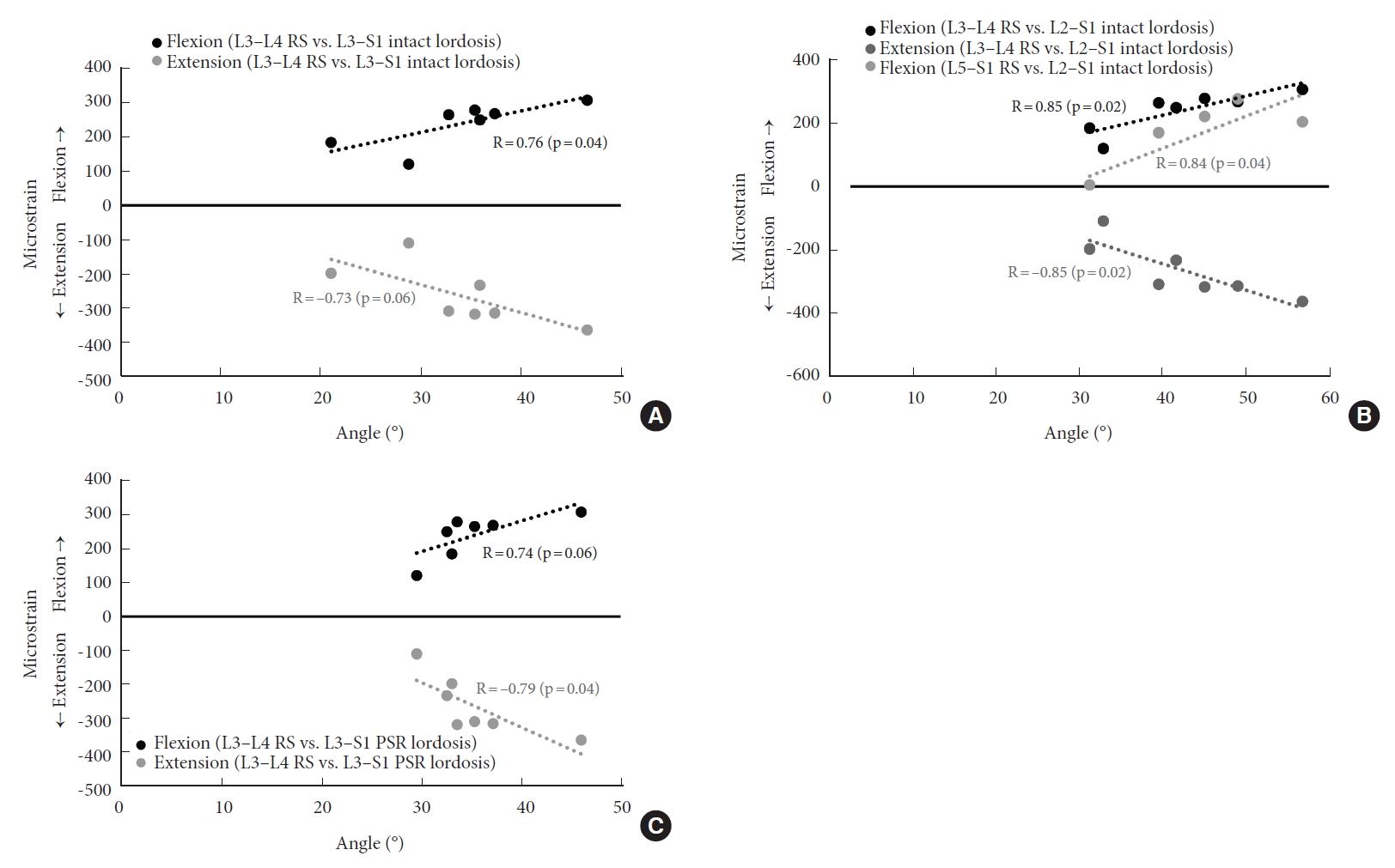
Fig. 4.
Photograph of a specimen instrumented with pedicle screws and rods on the testing frame showing how the rod is loaded. (A) 7.5 Nm pure moment in extension is represented by the arrow. (B) Pure moment couple in 2 opposing vertical load vectors is represented by arrows and separated by 7.5 cm (horizontal line). Adapted with permission from Barrow Neurological Institute, Phoenix, AZ, USA.

Fig. 5.
(A) Flexion-extension models simulating a 150-mm long, 5.5-mm diameter titanium alloy rod fixed at the distal end, with a slight curve (model I) and a more lordotic curve (model II), subjected to axial loads as seen during construct bending (see Fig. 4, tensile during flexion, compressive during extension). The blue arrows indicate applied forces (input), and green arrows indicate reaction forces (output, equal and opposite). (B) Resulting maximum stresses for the same magnitude axial load. Model II (rod with more lordotic curvature) is subjected to a higher maximum stress than model I (rod with a less lordotic curvature). Simulations were performed using an online 2-dimensional finite element analysis calculator [33]. Elem, element; Fy, force along the y-axis; MPa, megapascal; N, Newton; Ry, resultant force along the y-axis. Adapted with permission from MechaniCalc, Inc.
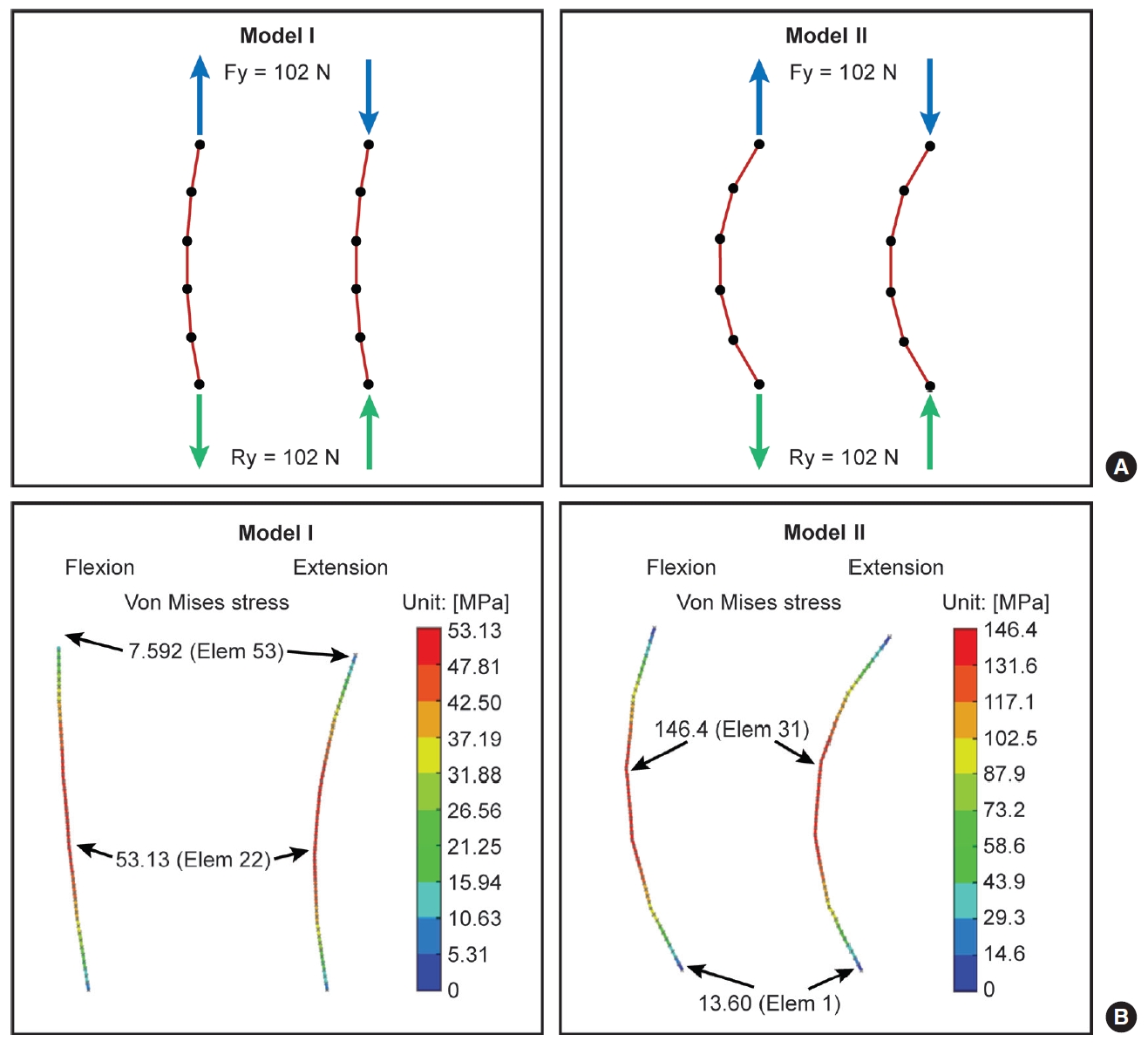
Table 1.
Demographic variables for cadaveric spinal segments
BMD, bone mineral density; BMI, body mass index; SD, standard deviation.
Data adapted from Godzik et al. Spine J 2020;20:465-74 [21].
Table 2.
Lordotic angles measured at different levels in intact and pedicle screws and rods (PSR) conditions
| Lordotic angle | Intact | PSR | p-value |
|---|---|---|---|
| L1-S1 lordosis | 54.91 ± 14.61 | 53.51 ± 9.86 | 0.76 |
| L2-S1 lordosis | 45.80 ± 11.88 | 43.84 ± 9.34 | 0.51 |
| L3-S1 lordosis | 36.91 ± 10.55 | 36.55 ± 6.05 | 0.89 |
| L4-S1 lordosis | 29.68 ± 6.00 | 25.46 ± 5.02 | 0.01* |
| L5-S1 lordosis | 7.36 ± 7.02 | 7.22 ± 4.12 | 0.95 |
Table 3.
Strain peak mean values
Table 4.
Correlations between different lumbar lordosis angles and rod strain during different conditions by direction of loading
| Specimen ID |
Lordosis |
Rod strain |
Direction of loading | R | p-value | ||
|---|---|---|---|---|---|---|---|
| Spinal level | Spine condition | Spinal level | Spine condition | ||||
| 1 | L2–S1 | Intact | L3–L4 | PSR | Flexion | 0.85 | 0.02* |
| 2 | L2–S1 | Intact | L3–L4 | PSR | Extension | -0.85 | 0.02* |
| 3 | L2–S1 | Intact | L5–S1 | PSR | Flexion | 0.84 | 0.04* |
| 4 | L3–S1 | Intact | L3–L4 | PSR | Flexion | 0.76 | 0.04* |
| 5 | L3–S1 | Intact | L3–L4 | PSR | Extension | -0.73 | 0.06† |
| 6 | L3–S1 | PSR | L3–L4 | PSR | Flexion | 0.74 | 0.06† |
| 7 | L3–S1 | PSR | L3–L4 | PSR | Extension | -0.79 | 0.04* |
REFERENCES
1. Roussouly P, Berthonnaud E, Dimnet J. Geometrical and mechanical analysis of lumbar lordosis in an asymptomatic population: proposed classification. Rev Chir Orthop Reparatrice Appar Mot 2003 89:632-9.

2. Sing DC, Berven SH, Burch S, et al. Increase in spinal deformity surgery in patients age 60 and older is not associated with increased complications. Spine J 2017 17:627-35.


3. Schwab F, Dubey A, Gamez L, et al. Adult scoliosis: prevalence, SF-36, and nutritional parameters in an elderly volunteer population. Spine (Phila Pa 1976) 2005 30:1082-5.


4. Glassman SD, Bridwell K, Dimar JR, et al. The impact of positive sagittal balance in adult spinal deformity. Spine (Phila Pa 1976) 2005 30:2024-9.


5. Blondel B, Schwab F, Ungar B, et al. Impact of magnitude and percentage of global sagittal plane correction on health-related quality of life at 2-years follow-up. Neurosurgery 2012 71:341. -8. discussion 8.


6. Roussouly P, Pinheiro-Franco JL. Sagittal parameters of the spine: biomechanical approach. Eur Spine J 2011 20 Suppl 5:578-85.


7. Roussouly P, Pinheiro-Franco JL. Biomechanical analysis of the spino-pelvic organization and adaptation in pathology. Eur Spine J 2011 20 Suppl 5:609-18.


8. Roussouly P, Gollogly S, Berthonnaud E, et al. Classification of the normal variation in the sagittal alignment of the human lumbar spine and pelvis in the standing position. Spine (Phila Pa 1976) 2005 30:346-53.


9. Le Huec JC, Aunoble S, Philippe L, et al. Pelvic parameters: origin and significance. Eur Spine J 2011 20 Suppl 5:564-71.


10. Le Huec JC, Charosky S, Barrey C, et al. Sagittal imbalance cascade for simple degenerative spine and consequences: algorithm of decision for appropriate treatment. Eur Spine J 2011 20 Suppl 5:699-703.


11. Vaz G, Roussouly P, Berthonnaud E, et al. Sagittal morphology and equilibrium of pelvis and spine. Eur Spine J 2002 11:80-7.


12. Maruo K, Ha Y, Inoue S, et al. Predictive factors for proximal junctional kyphosis in long fusions to the sacrum in adult spinal deformity. Spine (Phila Pa 1976) 2013 38:E1469-76.


13. Pizones J, Moreno-Manzanaro L, Sanchez Perez-Grueso FJ, et al. Restoring the ideal Roussouly sagittal profile in adult scoliosis surgery decreases the risk of mechanical complications. Eur Spine J 2020 29:54-62.


14. Zhang G, Yang Y, Hai Y, et al. Analysis of lumbar sagittal curvature in spinal decompression and fusion for lumbar spinal stenosis patients under roussouly classification. Biomed Res Int 2020 2020:8078641.



15. Guler UO, Cetin E, Yaman O, et al. Sacropelvic fixation in adult spinal deformity (ASD); a very high rate of mechanical failure. Eur Spine J 2015 24:1085-91.


16. Tang JA, Leasure JM, Smith JS, et al. Effect of severity of rod contour on posterior rod failure in the setting of lumbar pedicle subtraction osteotomy (PSO): a biomechanical study. Neurosurgery 2013 72:276. -82. discussion 83.

17. Hallager DW, Gehrchen M, Dahl B, et al. Use of supplemental short pre-contoured accessory rods and cobalt chrome alloy posterior rods reduces primary rod strain and range of motion across the pedicle subtraction osteotomy level: an in vitro biomechanical study. Spine (Phila Pa 1976) 2016 41:E388-95.

18. Newcomb A, Turner JD, Kelly BP. Letter to editor: strain in posterior instrumentation resulted by different combinations of posterior and anterior devices for long spine fusion constructs. Spine Deform 2018 6:334-5.


19. Kleck CJ, Illing D, Lindley EM, et al. Reply to letter to editor: strain in posterior instrumentation resulted by different combinations of posterior and anterior devices for long spine fusion constructs. Spine Deform 2018 6:335-40.


20. Tsuchiya K, Bridwell KH, Kuklo TR, et al. Minimum 5-year analysis of L5-S1 fusion using sacropelvic fixation (bilateral S1 and iliac screws) for spinal deformity. Spine (Phila Pa 1976) 2006 31:303-8.


21. Godzik J, Pereira BA, Newcomb A, et al. Optimizing biomechanics of anterior column realignment for minimally invasive deformity correction. Spine J 2020 20:465-74.


22. Kelly BP, Bennett CR. Design and validation of a novel Cartesian biomechanical testing system with coordinated 6DOF real-time load control: application to the lumbar spine (L1-S, L4-L5). J Biomech 2013 46:1948-54.


23. Panjabi MM. Biomechanical evaluation of spinal fixation devices: I. A conceptual framework. Spine (Phila Pa 1976) 1988 13:1129-34.

24. Panjabi MM, Abumi K, Duranceau J, et al. Biomechanical evaluation of spinal fixation devices: II. Stability provided by eight internal fixation devices. Spine 1988 13:1135-40.


25. Crawford NR, Dickman CA. Construction of local vertebral coordinate systems using a digitizing probe. Technical note. Spine 1997 22:559-63.


26. Godzik J, Hlubek RJ, Newcomb A, et al. Supplemental rods are needed to maximally reduce rod strain across the lumbosacral junction with TLIF but not ALIF in long constructs. Spine J 2019 19:1121-31.


27. Hlubek RJ, Godzik J, Newcomb A, et al. Iliac screws may not be necessary in long-segment constructs with L5-S1 anterior lumbar interbody fusion: cadaveric study of stability and instrumentation strain. Spine J 2019 19:942-50.


28. Sparrey CJ, Bailey JF, Safaee M, et al. Etiology of lumbar lordosis and its pathophysiology: a review of the evolution of lumbar lordosis, and the mechanics and biology of lumbar degeneration. Neurosurg Focus 2014 36:E1.

29. Labelle H, Roussouly P, Berthonnaud E, et al. The importance of spino-pelvic balance in L5-S1 developmental spondylolisthesis: a review of pertinent radiologic measurements. Spine (Phila Pa 1976) 2005 30:S27-34.
30. Galbusera F, Wilke HJ, Brayda-Bruno M, et al. Influence of sagittal balance on spinal lumbar loads: a numerical approach. Clin Biomech (Bristol, Avon) 2013 28:370-7.


31. Keller TS, Colloca CJ, Harrison DE, et al. Influence of spine morphology on intervertebral disc loads and stresses in asymptomatic adults: implications for the ideal spine. Spine J 2005 5:297-309.


32. Cunningham BW, Polly DW Jr. The use of interbody cage devices for spinal deformity: a biomechanical perspective. Clin Orthop Relat Res 2002 394:73-83.

33. MechaniCalc I. D Finite Element Analysis (FEA) [Internet]. Brooklyn (NY, MechaniCalc, Inc.. 2014-2021 [cited 2020 Jul 17]. Available from: https://mechanicalc.com/calculators/finite-element-analysis/.
































